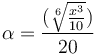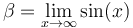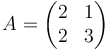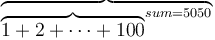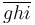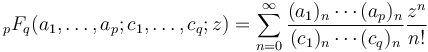提供: いつきメモ
(→数式テスト) |
(→いつきの考える勝手な才能の定式化) |
||
| (同じ利用者による、間の1版が非表示) | |||
| 行8: | 行8: | ||
# <math>\overbrace{\overbrace{ 1+2+\cdots+100 }^{sum=5050}}</math> | # <math>\overbrace{\overbrace{ 1+2+\cdots+100 }^{sum=5050}}</math> | ||
# <math>\overline{g h i}</math> | # <math>\overline{g h i}</math> | ||
| − | # | + | # <math>{}_pF_q(a_1,\dots,a_p;c_1,\dots,c_q;z) = \sum_{n=0}^\infty \frac{(a_1)_n\cdots(a_p)_n}{(c_1)_n\cdots(c_q)_n} \frac{z^n}{n!}</math> |
| + | |||
| + | == いつきの考える勝手な才能の定式化 == | ||
| + | ある能力に対する才能値を<math>s</math>とし、才能があると呼ばれる境界値を<math>S</math>と置く。 | ||
| + | つまり、常時<math>S \leq s</math>の状態を維持している状態を「才能がある人」と定義する。 | ||
| + | |||
| + | 才能値<math>s</math>に対し、１単位当たりの<math>s</math>上昇を<math>\Delta u</math>、１日当たりの<math>s</math>下降を<math>\Delta d</math>と置く。 | ||
| + | |||
| + | これは、例えば楽器演奏の才能に対し、１時間練習することで、演奏能力が<math>\Delta u</math>上昇し、１日たつ毎に演奏能力が<math>\Delta d</math>下降する事を意味する。 | ||
| + | |||
| + | つまり、「才能がある人」とは、<math>S \leq s = s_{start} + \sum(n_{times} \times \Delta u - \Delta d)</math>を維持している人の事である。<math>s_{start}</math>は各人が生まれ持つ初期値である。 | ||
| + | |||
| + | この定式化により、次のことが明らかとなる | ||
| + | # 限られたごく一部の例外（<math>S \leq s_{start}</math>が成り立つ人）を除き、 | ||
| + | ## １単位当たりの上昇<math>\Delta u</math>を行わない人は、<math>S</math>には永久に到達できない。 | ||
| + | ## １単位の上昇回数<math>n_{times}</math>を多く行った人の方がより<math>S</math>に到達できる可能性が上がる。 | ||
| + | # どれだけ多くの上昇を行っても、<math>S</math>に到達できない人がいる(<math>n_{times} \times \Delta u \leq \Delta d</math>) | ||
| + | # いわゆる天才型は<math>\Delta d</math>が小さい。逆に秀才型は<math>\Delta u</math>が大きい。 | ||
| + | |||
| + | これらから、ある才能に関して、それが趣味として成り立つためには、自己満足度<math>s_{my}</math>及び使用できる時間<math>n_{my}</math>に関して、以下の式が成り立つ必要がある | ||
| + | |||
| + | * <math>n_{my} \times \Delta u \geq \Delta d</math> | ||
| + | |||
| + | コレが成り立たない場合、自己満足度<math>s_{my}</math>に対し、<math>s_{my} \leq s (= s_{start} + \sum(n_{my} \times \Delta u - \Delta d))</math>が成り立たない。 | ||
| + | |||
| + | このため、才能が自己満足度<math>s_{my}</math>を超えることが無く、満足感を得ることが出来ない。 | ||
| + | |||
| + | 逆に、ある趣味の自己限界もこの式（<math>n_{my} \times \Delta u \geq \Delta d</math>）より導くことが出来る。 | ||
| + | |||
| + | 自分がかけられる時間×単位時間の能力上昇 ＜ １日当たりの能力下降 が成り立つ場合、その趣味はやめた方が賢明であろう。 | ||
2015年5月26日 (火) 16:55時点における最新版
ここはいつきが色々テストするページです
- 中身に意味はありません
数式テスト
いつきの考える勝手な才能の定式化
ある能力に対する才能値を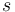
とし、才能があると呼ばれる境界値を
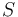と置く。
つまり、常時
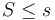の状態を維持している状態を「才能がある人」と定義する。
才能値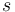に対し、１単位当たりの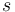上昇を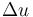
、１日当たりの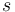下降を
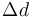と置く。
これは、例えば楽器演奏の才能に対し、１時間練習することで、演奏能力が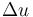上昇し、１日たつ毎に演奏能力が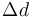下降する事を意味する。
つまり、「才能がある人」とは、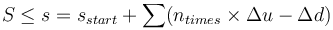
を維持している人の事である。
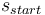は各人が生まれ持つ初期値である。
この定式化により、次のことが明らかとなる
- 限られたごく一部の例外（
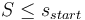が成り立つ人）を除き、
- １単位当たりの上昇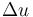を行わない人は、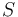には永久に到達できない。
- １単位の上昇回数
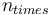を多く行った人の方がより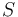に到達できる可能性が上がる。
- １単位当たりの上昇
- どれだけ多くの上昇を行っても、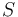に到達できない人がいる(
) - いわゆる天才型は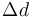が小さい。逆に秀才型は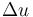が大きい。
これらから、ある才能に関して、それが趣味として成り立つためには、自己満足度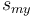
及び使用できる時間
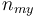に関して、以下の式が成り立つ必要がある
コレが成り立たない場合、自己満足度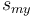に対し、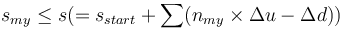
が成り立たない。
このため、才能が自己満足度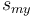を超えることが無く、満足感を得ることが出来ない。
逆に、ある趣味の自己限界もこの式（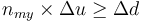
）より導くことが出来る。
自分がかけられる時間×単位時間の能力上昇 ＜ １日当たりの能力下降 が成り立つ場合、その趣味はやめた方が賢明であろう。